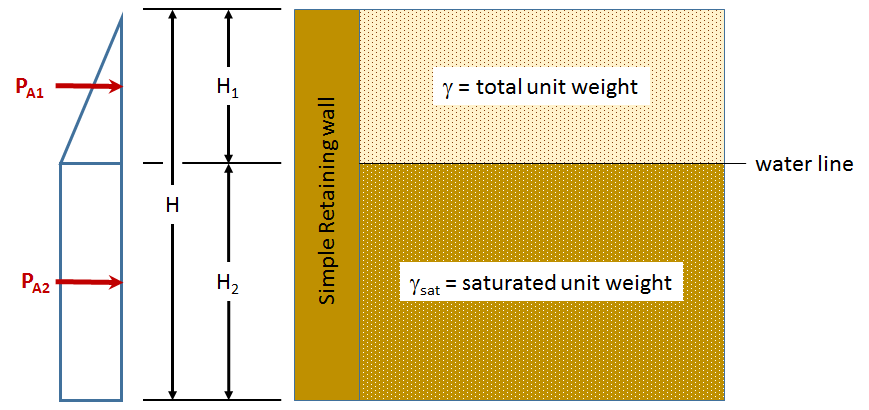
Horizontal Stress on Simple Retaining Wall
This equation computes the active horizontal soil pressure on a retaining wall. This equation assumes no cohesion between the soil behind the wall and the surface of the wall and it assumes the wall is vertical.
The inputs are:
- `gamma` - the total unit weight or weight density of the soil.
- `phi` - the angle of shear resistance phi characteristics of the soil
- `H_1` - the soil depth above the water line
Horizontal Stress (σh): The output horizontal stress or soil pressure is reported in units of Pascal
The Math / Science
The computation of horizontal soil pressure, active pressure, is based here on the Rankine Theory. This theory treats the soil to be in a state of plastic equilibrium.
The shear strength and stiffness of soil determines how stable the soil will be and how much it will deform. Calculating shear strength is used to determine if a slope is stable, if a structure might settle into the ground, and the limiting pressures on a retaining wall.
Soil is a composite of many particles that have little to no cementation. The shear strength of soil is primarily due to inter-particle friction. This means that the shear resistance on a plane is approximately proportional to the effective normal stress on that plane. The angle of internal friction is thus directly related to the maximum stable slope angle, often called the angle of repose.
A Retention Wall is a vertical or diagonal wall structure used to retain soil or water at an elevated height on one side of the wall, keeping it above the natural level that the soil or water would achieve. Retention walls are used to create relatively flat areas such as roads or gardens that are cut into a hillside. Retention walls are also used as levees to keep water out of an area. The soil and moisture on one side of the wall exerts pressure (stress) on the wall. This is why the materials used must be appropriate for the application in both density and porosity.